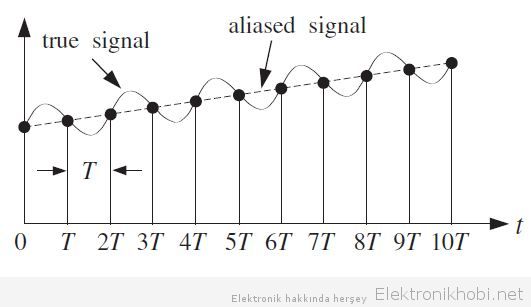
Bir önceki yazımızda da bahsettiğimiz üzere,eğer uygun örnekleme frekansıyla analog-dijital dönüşümü yapmazsak bilgi kayıpları,bozulmalar (gürültü vb gibi) olacaktır ve biz bu dijital verileri tekrar analog sinyallere dönüştürdüğümüzde aynı sinyal çıktısını elde edemeyeceğiz. Bu soruna “aliasing” denilir ve bunu önlemek için Nyquist teoremi doğrultusunda uygun frekans değerleriyle örnekleme işlemi yapılır. Aliasing sorununa bir örnekle açıklık getirelim:
Yukarıdaki grafikte analog sinyal ve örneklenmiş hali görülmekte. Uygun periyotta örnekleme yapılmadığı için dalgalı bir yapı gösteren sinyalin örneklenmiş formu lineer bir şekil almakta, örneklenen veriler sinyalin doğru şeklini yansıtmamaktadır.
İşte bir analog sinyali u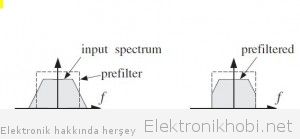
ygun örnekleme frekansıyla ayrıklaştırmak ve Nyquist teoreminin gereklerini sağlamak için, sinyal bir alçak geçiren (low-pass) filtreden geçirilir, bu işlemi gören filtrelere “anti-aliasing (takıntı-kesen)” filtre denir. Filtrenin kesme frekansı yani fmax, teoremin de bize söylediği gibi fs/2 veya daha küçük bir değere eşit olmalıdır. Sonuçta filtre çıkışındaki sinyalin bant genişliği max frekansa eşit olmuş olur. bundan sonra uygun örnekleme işlemi yapılabilir. Yandaki şekilde input spektrumu analog sinyalimizi ve kesikli spektrum da filtremizi ifade ederse,soldaki grafikte filtre dışında kalan fazlalık kısımlar Nyquist frekansını aşan kısımlar olup filtreleme sonrası bu kısımlar çıkartılır ve sağdaki ayrıklaştırma işlemine hazır forma getirilir.
Bu noktada yeri gelmişken bir konuya parantez açalım. Nyquist teoremi bize örnekleme frekansının alt limit değeri olan 2fmax<fs bilgisini vermekte ancak karşımıza şöyle bir soru daha çıkmakta. Peki fs nin üst limit frekansı olmalı mıdır? Evet olmalıdır çünkü eğer fs büyürse,zaman periyodu küçülür ve sinyal daha sık zaman aralıklarıyla örneklenir ve işlenecek bir sürü dijital veri ortaya çıkar. Bu noktada yeterli donanım etkinliği (donanımın veri işleme kapasitesi) sağlanmazsa kayıplar oluşacaktır. Bu sebepten dolayı, donanımın dataları işleme periyodu,örnekleme periyoduna eşit veya daha küçük olmalıdır. Frekans,periyodun tersi olduğuna göre, “işleme frekansı örnekleme frekansına eşit veya daha büyük olmalı” diyebiliriz. Böylelikle üst limiti de elde etmiş olduk.Sonuç olarak,donanım frekansına fp dersek 2fmax ≤ fs ≤ fp olur.
Low-pass filtrelerin kullanı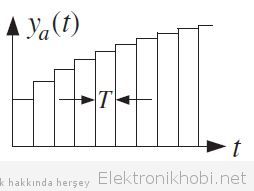
ldığı bir başka nokta ise dijitalden analoğa dönüştürme esnasındadır. Ayrık (discrete) sinyaller bir dijital-analog dönüştürücüyle birleştirilerek sürekli (analog) sinyale dönüştürüldükten sonra yandaki grafikte görüldüğü formu alır. Bu şekilde basamak basamak oluşmasının sebebi her bir dijital örneğin bit değerinin yansıtılmasından kaynaklanmaktadır. Bu konuyu bir sonraki yazımızda kapsamlı olarak ele alacağız.
Bu formda bir sinyal pek da orijinal analog sinyalle uyuşmamakta,işte bu noktada yine bir low-pass filtre devreye girer ve bize istenen çözümü sunar. Adından da anlaşılacağı üzere, low-pass yani alçak-geçiren filtreler, sinyalimizin yüksek frekanstaki istemediğimiz kısımlarını çıkartarak uygun frekans değerindeki sinyali meydana getirir.
Son olarak not düşmekte fayda var, pratik hayatta kullanılan low-pass filtreler ideal filtreler değillerdir dolayısıyla hiçbir zaman Nyquist frekans aralığı dışındaki bütün frekans bileşenlerini çıkartamazlar. Bu sebepten dolayı, uygun bir filtre dizaynı yapılarak çok daha az kayıpla tolore edilebilir sonuçlar elde edilmektedir.
Bir sonraki yazımız analogdan dijitale dönüşüm işleminde örneklenen sinyallerin ölçeklendirilip bitlere atanması (Quantization) hakkında olacak.
