TEK GÖZLÜ VE TEK TEMEL DÜĞÜM NOKTALI DEVRE ANALİZİ
Bu bölümde, Kirchhoff’un akım ve gerilim yasalarının, tek bir gözden veya tek temel düğüm noktasından oluşmuş devreler için uygulamaları ele alınacaktır.
Tek Gözlü Devre Analizi
Tek gözlü devre analizi uygulamalarının esası, aslında o göz için Kirchhoff’un gerilim yasasını uygulamaktan ibarettir. Kirchhoff’un gerilim yasası, tek gözlü devrelerde, bağımlı ve bağımsız kaynak kullanımlarında da geçerlidir.
Aşağıda verilen devrede V1 > V2 olduğu kabul edilmektedir.
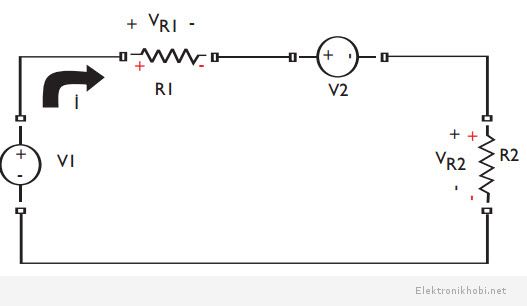
Yukarıda verilen devreye Kirchhoff’un gerilim yasası uygulanırsa,
olarak elde edilir.
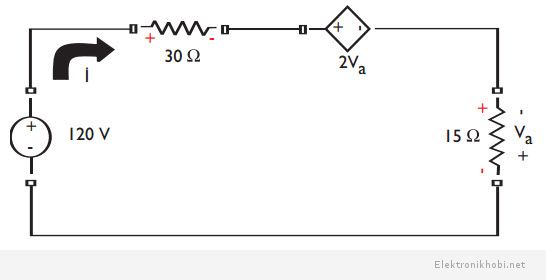
Örnek: Şekil 2.3’deki devre için V1 = 120 V, V2 = 30 V, R1= 30 Ωve R2 = 15 Ωise ana koldan geçen akımı ve her elemanın harcadığı ya da sağladığı gücü bulunuz.
Çözüm:

Örnek: Aşağıdaki devrede i akımını bulunuz.
Çözüm :
Devreye, Kirchhoff’un gerilim yasası uygulanırsa, -120 + 30i +2ϑa+15i = 0
olarak elde edilir.
Öte yandan tanımlı olan Va gerilimi ile i arasında, Va= -15i şeklinde bir ilişki söz konusudur. Burada tanımlı olan i akımı, 15 Ω’luk direnç
üzerinde 15i şeklinde bir gerilim oluşturmakla birlikte, pasif elemanlar üzerinde oluşan gerilim göz önüne alındığında, ters polariteye sahip bir Va
gerilimini oluşturur. Bu durum, eşitlikte negatif katsayısı kullanımı anlamına gelir. Bu durum Kirchhoff’un gerilim yasası denkleminde yerine yazılırsa,
-120 + 30i – 30i + 15i = 0 ve i=8 A olarak elde edilir.
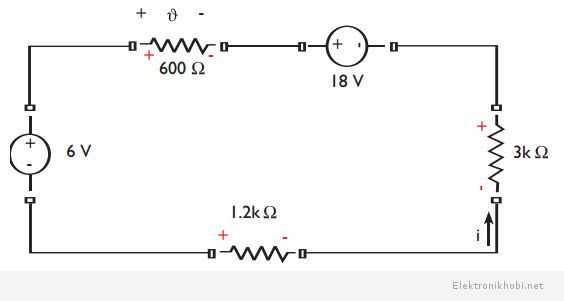
Örnek:
Aşağıdaki devre için
a)i akımını,
b)ϑgerilimini,
c)6 V’luk kaynağın sağladığı gücü bulunuz.
Burada, 6 V’luk kaynak, akım yönüne göre terstir. Bu durumda kaynağın pasif eleman gibi davrandığına dikkat edilmelidir.
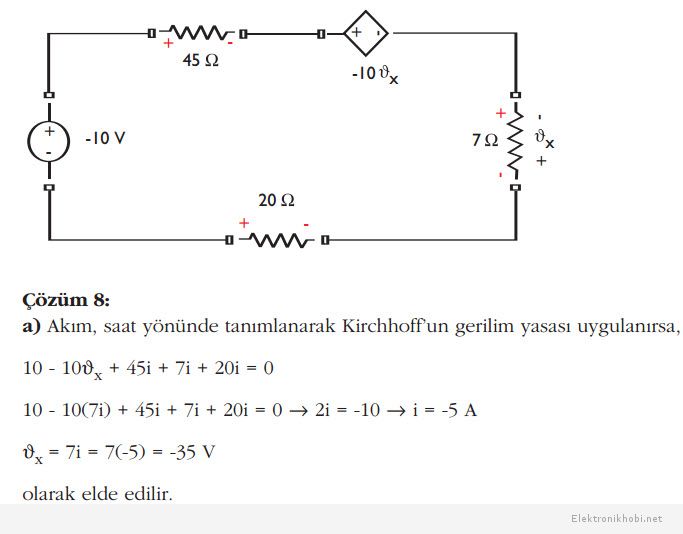
Örnek: Aşağıdaki devre için
a) ϑx,
b) Bağımsız kaynak tarafından sağlanan gücü,
c) Bağımlı kaynak tarafından sağlanan gücü
bulunuz.
Tek Temel Düğüm Noktalı Devre Analizi
Tek temel düğüm noktalı devre analizi uygulamalarının esası, aslında ilgili düğüm noktası için Kirchhoff’un akım yasasını uygulamaktan ibarettir.
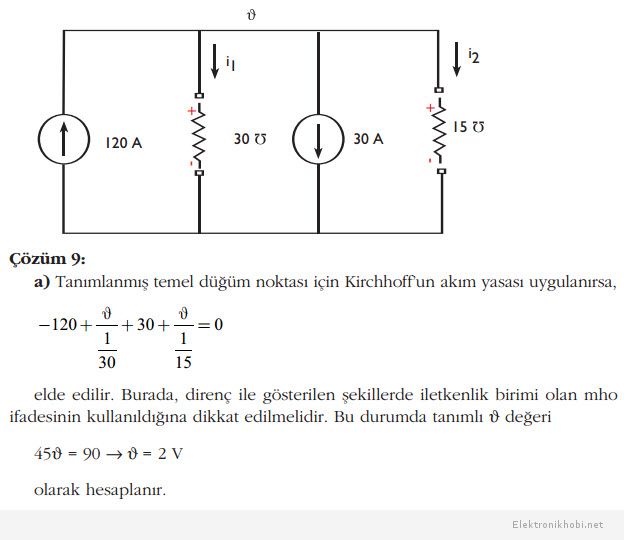
Örnek: Aşağıdaki devre için
a) ϑgerilimini,
b) i1 ve i2 akımlarını,
c) Her elemanın sağladığı/harcadığı gücü bulunuz.

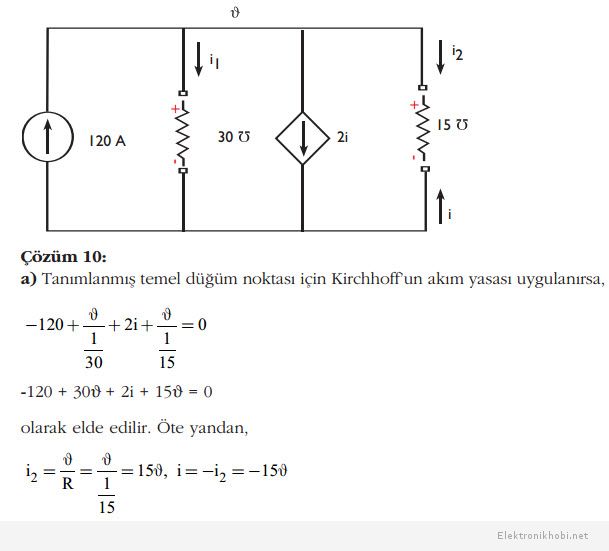
Örnek: Aşağıdaki devre için
a) ϑ gerilimini,
b) i akımını
bulunuz.

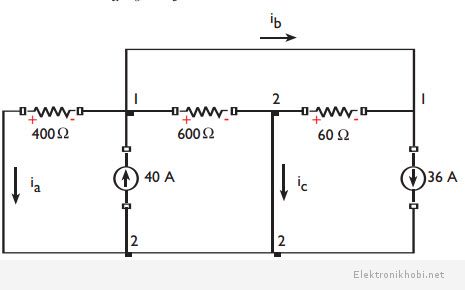
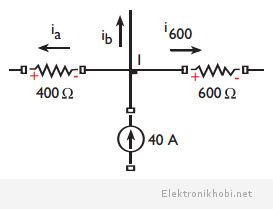
Örnek: Şekildeki devrede ia, ib ve ic akımlarını bulunuz.
Çözüm :
Şekil incelendiğinde, 1 ve 2 numaralı düğüm noktalarını yeniden düzenleyerek problemi çözmek daha kolay olacaktır. 1. temel düğüm noktası gerilimiϑolarak
tanımlanırsa, problem aşağıdaki gibi tek düğüm noktalı devre haline dönüşür. 2. düğüm noktası ise, referans olarak belirlenmiştir.
şeklinde hesaplanabilir. Burada, 600 Ω ve 60 Ω’un üzerinden geçen akımlar, 1. temel düğüm noktasından 2. düğüm noktasına (referans) doğrudur. Aşağıdaki şekilde 1. temel düğüm noktasına giren ve çıkan akımlar gösterilmektedir.

Örnek: Şekildeki devrede i akımını bulunuz.
Çözüm :
1 ve 2 numaralı düğüm noktalarını yeniden düzenleyerek problemi çözmek daha kolay olacaktır. 1. temel düğüm noktası gerilimiϑolarak tanımlanırsa, problem
aşağıdaki gibi tek düğüm noktalı devre haline dönüşür. 2. düğüm noktası ise, referans olarak belirlenmiştir.

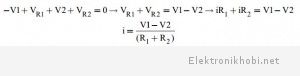








s.a abim son sorudaki işlemlerde 120 voltu nasıl buluyoruz açıklarsanız çok iyi olur saolun.