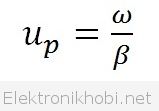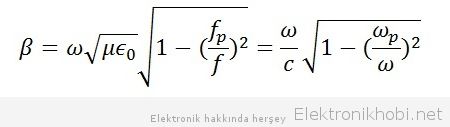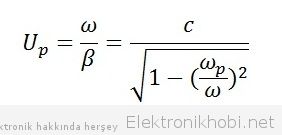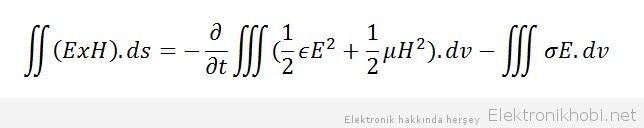Grup ve Faz Hızları
Haberleşmede kullandığımız sinyallerin bir çoğu band frekansı içermektedir. Yani sinyalin içinde yüksek taşıyıcı frekansın etrafında yayılmış küçük frekanslar vardır. Bu küçük frekanslar forrier transform işlemi ile dalga bileşenlerine ayrılarak matematiğe dökülebilir.
Bir elektromanyetik dalganın faz katsayısı olarak bilinen Phase constant (β) yani dalganın ilerleme kat sayısının complex bileşeni, dalganın faz hızı ile ilişkilidir.
Bir dalga paketinin(Sinyalin) içerisinde farklı frekanslara ve farklı faz hızlarına sahip olan elektromanyetik dalgalar sinyalin daha çabuk bozulmasına sebep olurlar. Bu olaya gavurlar disporsion olayı diyorlar yani sinyalin bozulması. Buna göre karşımıza iki hız kavramı çıkıyor. Birincisi sinyal paketinin frekans hızı ki buna grup hızı diyoruz. İkincisi ise faz hızıdır, bu da asıl frekansın dalga bileşenlerinin faz hızıdır.
Yukarıdaki giften de gördüğümüz gibi kırmızı nokta yani grup hızı ve mavi nokta yani faz hızı arasında farklılıklar söz konusudur. Faz hızının tam formülünü yazarsak;
Faz sabitinin formülüne bakarak şu çıkarımda bulunabiliriz, Faz frekansı grup frekansına eşit olduğunda faz sabitimiz sıfıra eşit oluyor yani bu durumda cut off frekansı elde etmiş oluyoruz. Grup frekansının faz frekansından büyük olduğunu düşünürsek bu sefer faz sabitimizi reel bir değer alacaktır ve bu dalgamızın ilerlemesi için yeterlidir. Fakat tam tersini düşündüğümüzde İlerleme sabitimizin complex bileşeni olacağından dalgamız ilerledikçe sönümlenecektir.
Aynı çıkarımı faz hızı ve grup hızlarının arasındaki ilişkiyi tanımlayan şu formülle de yapabiliriz;
Bu formüle baktığımızda; üç olasılık karşımıza çıkar
1-) Faz hızının açısal frekansa göre birinci türevi “0” olduğunda grup hızı ve faz hızı birbirine eşit olacaktır. Bu durumda dalga paketimiz bozulmaya uğramaz.
2-)Faz hızının açısal frekansa göre birinci türevi “0” dan küçükse, grup hızı faz hızından küçük olacaktır. Bu durumda dalgamız normal bozulmaya uğrar.
3-) Faz hızının açısal frekansa birinci türevi”0″ dan büyük olduğunda grup hızı faz hızından büyük olacaktır. Bu durumda dalga paketi anormal yani aşırı şekilde bozulmaya uğrar.
Elektromanyetik Güç Aktarımı ve Poying Vektör
Elektromanyetik dalgalar elektromanyetik güç taşırlar. Elektromayetik dalgaların taşıdığı bu güç yine maxwell’in elektromanyetik dalgaları tanımlayan denklemleri ile ifade edilir. Buna göre gerekli vektör operasyonları yapıldığında karşımıza şu sonuç çıkıyor;
Elektromanyetik güç; elektrik ve manyetik alanların curl ünün alan integraline eşittir. Eşitliğin sağ tarafındaki ilk ifade elektrik ve manyetik alanların depoladığı enerjiyi ikici ifade ise ohmic power density olarak bilinir ve elektromanyetik dalganın ortamda ilerlerken kaybettiği enerjiyi ifade eder.
Poyinting vektör birim alana düşen güç akısını temsil eder ve yukarıda da gördüğünüz gibi formülü şudur;