Konumuza giriş yapmadan önce sinyaller ve onların işlenmesi hakkında kısa bir bilgiyle başlayalım.
Bilindiği üzere sinyaller ikiye ayrılır: sürekli zamanlı (continious time ) ve ayrık zamanlı (discrete time) sinyaller. Analog sinyaller sürekli zamanlı, dijital sinyaller ise ayrık zamanlı sinyaller olarak kategorize edilir. Analog sinyallerin bilgisayar ve elektronik sistemlerinde değerlendirilebilmesi için onların dijital sinyallere dönüştürülmesi gereklidir, çünkü bu sistemler analog sinyalleri yorumlayamazlar .Yine dijital sinyaller de dış dünyada anlamlı ifadeler oluşturamazlar,bunların tekrar analog sinyallere dönüştürülmesi gerekir.
Şimdi buna bir örnek verelim: bir şarkıcı şarkı söylediğinde çıkardığı ses dış dünya için anlamlı olan analog sinyallerdir,bunları bilgisayara kaydederken sinyaller dijitale çevrilerek kaydedilir,çünkü bilgisayar için anlamlı olan format bu şekildedir. Biz bu şarkıyı dinlemek istediğimizde bilgisayar sakladığı bu dijital bilgiyi analog sinyallere çevirerek bizim için anlamlı olan formata çevirir. Bu işlemleri analog-dijital dönüştürücüler (AD Converter) ve dijital-analog dönüştürücüler (DA Convereter) yapar. Buraya kadar anlattığımız kısım ayrı bir yazı konusu olacak kadar uzun olduğundan ayrıntıya girmeden geçiyoruz.
Dijital Sinyal İşleme (Dijital Signal Processing) elektrik,elektronik ve bilgisayar biliminin önemli dallarından birisidir. Bu bilimdalı temel olarak üç aşamalı incelemeden oluşmaktadır:
1. Analog sinyallerin örneklenme (sampling) yoluyla dijitale çevrilmesi ve alınan her örneğin ölçeklendirilip bitlere atanması (quantization). Bu kısma genel olarak analog-dijital dönüşüm işlemi denir.
2. Dijital sinyallerin bir dijital sinyal işleyicisi (Dijital Signal Processor-DSP) ile işlenmesi (örneğin filtreleme vb. gibi)
3. Gerektiği zaman yeniden dijitalden analoğa dönüştürülmesi
Şimdi yazı başlığımız olan analog sinyallerin nasıl örnekleneceği konumuza başlayabiliriz.
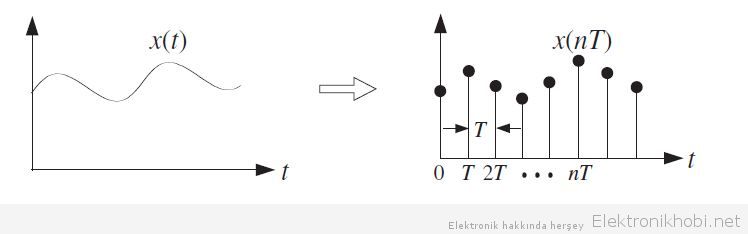
Grafikte de görüldüğü şekliyle bir analog sinyalin örneklenmesi belli zaman aralıklarıyla sinyalin değerlerinin ölçülmesi olayıdır. Sinyal t=nT n=0,1,2,3…. Zaman aralıklarıyla ayrıklaştırılmış ve ayrıl bir sinyal elde edilmiştir. Ortaya çıkan bu ayrık zamanlı sinyalin orijinal olan analog sinyalle örtüştüğü aşikardır yani bu noktaları birleştirdiğimiz zaman analog sinyalin aynısını elde edebilmekteyiz,mutlaka kayıplar olacaktır ancak önemli olan bunun tolore edilebilir olmasıdır.
Bu noktada akla şöyle bir soru gelmekte: ayrıklaştırma işleminde hangi zaman aralığında örnekleme yapılırsa kayıplar en aza indirilebiir? Şöyle bir cevap verebiliriz: ne kadar küçük alırsak o kadar sinyal varyasyonları kaybedilmemiş olur. Mümkün elbette ancak bu sefer de işlenmesi gereken çok fazla sayıda örnek alınmış olur. Şimdi bunu bir örnekle daha iyi açıklayalım.
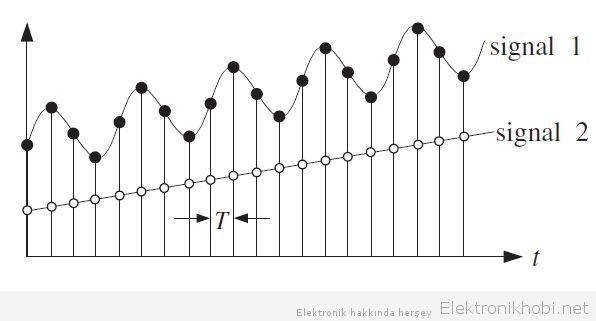
Grafikteki birinci sinyal uygun zaman aralıklarıyla örneklenmişdir ve analog sinyalden herhangi bir kayıp görülmemektedir.İkinci sinyal ise oldukça gereksiz bir fazlalıkta örneklenmiştir çünkü sinyalde zamana bağlı olarak herhangi bir varyasyon (bilgi kaybına yol açacak kısa uzun dalgalanmalar vb gibi şeyler ) gözlenmemektedir. O halde bu sinyalin örneklenme periyodu daha büyük alınabilir böylece gereksiz sinyal işlemeden kurtulmuş olunur.
İşte bu noktada geliştirilen örnekleme teoremi bize yapılması gereken iki şey olduğunu söyler:
1. Sinyalin bant genişliği belirlenmeli, yani frekans spektrumu (tayfı) olabilecek max bir frekans aralığında sınırlanmalı
2. Örnekleme frekansına fs dersek, fs ≥ 2fmax eşitliği sağlanmalı
Buna göre,minimum örnekleme frekansı fs=2fmax dır ve buna “Nyquist Değeri” denir ve herhangi bir fs değerinde fs/2 ye karşılık gelen değere de” Nyquist Frekansı” denir. İsveçli bir elektronik mühendisi olan Harry Nyquist bu teoremi bilim dünyasına kazandırmıştır.
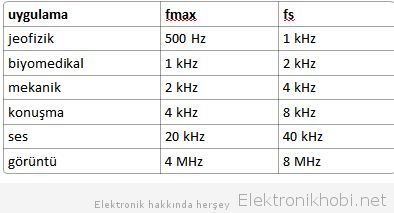
Bazı yaygın sinyal işleme uygulamalarının örnekleme frekansları tabloda verilmiştir:
Dijital Sinyal İşlemenin ilk aşamasına böylelikle giriş yapmış olduk.Bu konuda ilerlemeye devam edeceğiz,bir sonraki yazımız örnekleme sonrası aliasing sorunu ve onun giderilmesi noktasında kullanılan low-pass (alçak geçiren) filtreler olacak.
