Bir elektronik mühendisi olarak üniversite hayatım boyunca diferansiyel denklemler çözüp fiziksel eylemlerin matematiksel modellerini kullandım. Sistemlerin matematiksel olarak nasıl modellenebileceğini anlatan derslere girdim. Çoğu zaman kullandığım bu baş döndürücü matematiğin ne kadar inanılmaz olduğunu düşünemedim. Bazen gözünüzün önünde çok aşikar bir şekilde duran bir şeyi görebilmek için bulunduğumuz ortamın dışına çıkmanız gerekebiliyor.
Üniversitedeyken “EEE406-Analog Filter Design” isminde bir dersimiz vardı. Analog filtreler, radyolarda, telefonlarda, televizyonlarda ve bir çok cihazda frekans seçmek için kullanılan elektronik sistemleri içeriyor. Örneğin radyolarda her bir frekansta farklı bir yayın vardır. 100 MHZ de A radyo kanalını dinlerken 100.5 MHZ de farklı bir radyo kanalını dinliyoruz. Bu frekansları seçerek istediğimiz frekans üzerindeki sesi dinleyebilmek için bazı RL, RLC ve ya RL devrelere ihtiyacımız oluyor. Bu devreleri tasarlamak için kullandığımız bazı matematiksel yaklaşımlar ve matematiksel fonksiyonlar vardı. Onlardan bir tanesi Chebisev Fonksiyonuydu. Chebisev, matematikte olasılıkla uğraşmış ve bu branşla alakalı bazı teoremler geliştirmiş bir rus matematikçidir. Biz bu derste “Chebisev Fonksiyonunu analog filtreler tasarlamak için kullanmıştık. Çünkü bu fonksiyonlar analog filtrelerin karakteristik özelliklerini çok güzel bir şekilde matematiksel olarak tasvir ediyordu. Halbuki Chebisev fonksiyonu, analog filtreler tasarlamak için geliştirilmemişti. Chebisev, bu fonksiyonunu olasılıkla alakalı bir kaç problemin çözümü için geliştirmişti. Elektronik Mühendisleri bu fonksiyonu çok daha sonraları inceleyerek dizayn ettikleri sistemlerin karakteristiklerini tasvir ettiğini keşfettiler ve kendi çalışmalarında da bu fonksiyonu kullanmaya başladılar.


Bir başka örnek daha vereyim. Laplace transformunu kullanmayan çok az mühendis vardır. Mühendisler Laplace transformunu diferansiyel denklemlerin çözümlerinde kullanıyor. Diferansiyel deklemler, birbirine göre değişen değişkenlerin olduğu denklemlerdir. Örneğin bir arabanın hareketini düşünün. Arabanın hızı zamana göre değişiyorsa ve biz arabanın hızının ve zamanın olduğu bir denklem kurmak istiyorsak burada kurulması gereken denklem, diferansiyel bir denklem olmalıdır. Ve temel fizikteki “hız-hareket” konusunda kullanılan formüllerin çoğu diferansiyel denklemler ile geliştirilmiştir. Laplace transformunu ilk olarak “Simon Laplace” ismindeki astronomist geliştirmiştir. Simon’un amacı diferansiyel denklemleri çözmek değildi. Ve teoremi geliştirdiği yıllarda hiç kimsenin ilgisini çekmemişti. 2. dünya savaşından sonra , Leonhard Euler, bu dönüşümün diferansiyel denklemleri çözmek için kullanılabileceğini keşfetti ve bu dönüşüm yardımıyla diferansiyel denklemleri çözmeyi başardı. Halbuki Euler’in amacı da mühendislerin kullandığı denklemleri çözmesini sağlamak değildi. Bu gün diferansiyel denklemleri mühendisliğin her alanında sistemleri tanımlamak, davranışlarını öngörmek için kullanıyoruz.
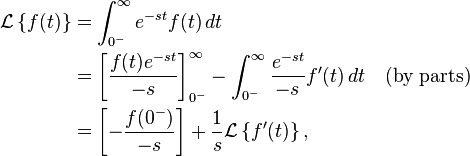
Matematikte diğer pozitif bilimlerde olmayan diğer bir özellik ise matematiksel doğrunun sonsuza kadar doğru olarak kalması ve değişmemesidir. Fizik, kimya ve biyoloji gibi pozitif bilimlerde çoğu zaman geliştirilen kuramlar daha sonraları yanlış olarak kabul edilebilir. Fakat matematikte belli kurallar bütününde kabul edilen doğrular, sonsuza dek doğrudur. Örneğin Pisagor teoremini herkes bir şekilde kullanmıştır. 2000 yıl önce dik üçgenin hipotenüs uzunluğunu bulak için kullanılan pisagor denklemi, bu gün de aynı şekilde kullanılıyor. İki artı iki toplamının sonucu hiç bir zaman beş olmayacaktır.
Evrendeki görüp dokunabildiğimiz bir çok şeyi matematiksel olarak tabir edebiliyoruz. Bu bize evreni ve olayları kavrayabilmemizi sağlıyor. Evrene matematiksel olarak baktığımızda kusursuz matematiksel bağlantıların olduğunu görüyoruz. Tüm düzenin matematiksel olarak sağlanabildiğine tanıklık ediyoruz. Kim bilir gelecekte belki de başka matematiksel teoremler yardımıyla hayal gücümüzü zorlayan başka fiziksel olguları kavrayabileceğiz. Öte yandan eğer matematik sadece insan zihninin oluşturduğu bir ürünse ve insan zihninin dışında herhangi bir varlığı yoksa nasıl oluyor da kainata ve sistemlere dair ancak yüzyıllar sonra sorulabilecek sorulara cevap verebiliyor?
Bunca şeyi düşündüğümüzde insan kendine matematiğin evreni bu kadar kusursuz bir şekilde nasıl tanımlayabildiğini sormadan edemiyor. Matematiği sadece insan zihninin oluşturduğu bir akıl oyunundan ibaret görmek çoğu zaman saçma geliyor. Bu yüzden yazının başlığını “Matematik Keşif mi yoksa İcat mı?” koydum.
Benim fikirlerimi soracak olursanız. Matematik Allah’ın insana bahşetmiş olduğu bir gerçekliktir. Aslında biz matematiği aynı uzayı keşfeder gibi keşfediyoruz…






Matematik insan var olmadan da vardı. O halde icat değildir bana göre.. Asıl soru şu olabilir: Mahluk mudur? (Yaratılmış mı? ) Yoksa ezelden beri var mıydı? Bu sorunun cevabı felsefe alanına giriyor. Yani kesin bir çözüm yoktur.